近期在整理样本量计算的课件,遇到z检验的相关概念原理,搜集一些资料如下:
Z分布(标准正态分布)
正态分布是有均值μ和标准差σ定义的一种概率分布;若一个连续随机变量X符合均值μ和标准差σ的正态分布,则写为X~N(μ,σ^2)。
如果均值μ=0,标准差σ=1,则X~N(0,1)符合标准正态分布。
实际上,对于一个正态分布,可以通过标准化转化为标准正态分布,转化方法是z=(x-μ)/σ,可通过概率分布函数证明。因此标准正态分布又称为z分布,是正态分布的一种。
什么是Z检验
Z检验用来判断样本均值是否与总体均值具有显著性差异的方法。通过正态分布理论来推断差异发生的概率,从而比较两个均值的差异是否显著。
Z检验的前提条件
(1)服从正态分布
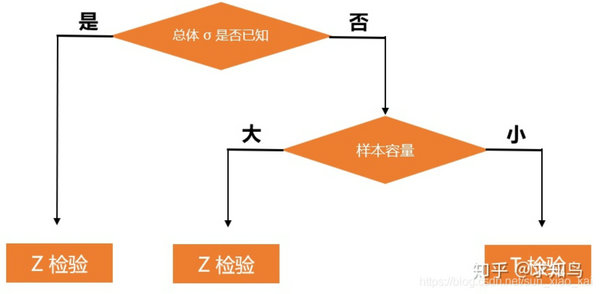
(2)总体标准差已知或样本量足够大(n>30)
===
Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率,从而比较两个平均数的差异是否显著。
当已知标准差时,验证一组数的均值是否与某一期望值相等时,用Z检验。另外,对于Z检验我国的统计学教材大多采用U检验的说法。而国外英文统计学书籍,大多采用Z检验。
Z检验的类型
(1)单样本均值z检验
检验一个样本平均数与一个已知的总体平 均数的差异是否显著。
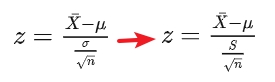
¯X为样本均值;μ为总体均值;σ为总体标准差;n为样本容量。
(2)双独立样本均值z检验
检验来自两个的两组样本平均数的差异性,从而判断它们各自代表的总体差异是否显著。
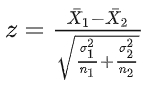
如果两个样本的总体标准差σ1、σ2未知,则可用样本标准差s1,s2代替。
¯X1、¯X2为两个样本数据的平均值;σ1、σ2为总体标准差;s1、s2为样本标准差;n1、n2为样本量。
(3)比例差异z检验
补充:两个独立样本比例之差的z检验(比例差异时通常用z检验)
===
两个总体比例之差的Z检验
假定条件:
1.两个总体独立
2.两个总体都服从正态分布
3.可以用正态分布来近似(当n趋于无穷是的二项分布)
===
率的z检验-两样本率比较,采用Z检验的条件是两个样本含量n1与n2均较大,且p1与p2均不接近于0也不接近于1,一般要求n1 p1、n1(1——p1)、n2 p2及n2 (1——p2)均大于5。
===
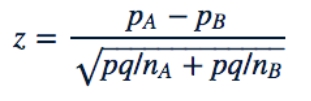
pA 是在A组中观察到的比例值,其中样本数为nA
pB是在B组中观察到的比例值,其中样本数为nB
p和 q 是总比例值(无论A、B组)
请注意,z统计量的公式仅在样本数量(n)足够大时适用。即nA*p,nA*q,nB*p和nB*q都要≥ 5。
z检验与卡方检验区别
z检验是参数检验方法,卡方检验是非参数检验方法。
卡方检验就是统计样本的实际观测值和理论推断值之间的偏离程度,偏离程度决定卡方值的大小,卡方值越大,二者偏离程度越大;如果两个值完全相同则卡方值为0。卡方检验是非参数检验,适用于布尔型数据和二项分布数据。
卡方检验针对分类变量。可用于推断两个或两个以上总体率或构成比是否有差别等,多用于拟合优度检验和独立性检验。